January 2019 – Sisi Tang

January 31, 2019August 3, 2019

Derivation of Black-Scholes-Merton Formula

The derivation of the Black-Scholes-Merton formula is very clearly organized in section 4.5 of Shreve’s Stochastic Calculus for Finance II Continuous-Time Models. It is the most intuitive and clearest way that the author has seen so far. So, this part especially the organization of the article is borrowed from it though not identical.

Evolution of portfolio value

Let $X(t)$ represent the portfolio value at time $t$ .

We hold $\Delta(t)$ shares of the stock at time $t$ , and put the rest of money in money market with interest rate $r$ . Note that $\Delta(t)$ is adapted to the natural filtration of $W(t)$ . Then, the change of portfolio value is the change in stock plus the interest from money market. To be specific $X(t)$ satisfies the following SDE:

(1) $\begin{equation*} \ud X(t) = \Delta(t)\ud S(t) + r(X(t)-\Delta(t)S(t))\ud t \end{equation*}$

We plug Geometric Brownian motion $S(t)$ into this equation,

$\begin{aligned}\ud X(t) &= \Delta(t)(\alpha S(t) \ud t + \sigma S(t) \ud W(t)) + r(X(t)-\Delta(t)S(t))\ud t \\&= rX(t)\ud t + \Delta(t)(\alpha-r)S(t)\ud t + \Delta(t)\sigma S(t)\ud W(t).\end{aligned}$

The SDE of the discounted stock value $e^{-rt}S(t)$ is obtained by Ito’s formula.

(2) $\begin{equation*}\begin{aligned}\mathrm{d}(e^{-rt}S(t)) &= -re^{-rt}S(t) \mathrm{d} t + e^{-rt} \mathrm{d} S(t) + 0 + 0 + 0 \\&= -re^{-rt}S(t) \mathrm{d} t + e^{-rt} (\alpha S(t) \mathrm{d} t + \sigma S(t) \mathrm{d} W(t)) \\&= (\alpha-r)e^{-rt}S(t) \mathrm{d} t + \sigma e^{-rt} S(t) \mathrm{d} W(t)\end{aligned}\end{equation*}$

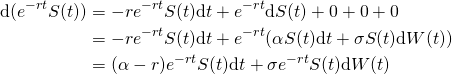
This equation says that discounting the stock price reduces the mean return rate from $\alpha$ to $\alpha-r$ .

Similarly, the SDE of the discounted portfolio value $e^{-rt}X(t)$ is

(3) $\begin{equation*}\begin{aligned}\mathrm{d} (e^{-rt}X(t))& = -re^{-rt}X(t) \mathrm{d} t + e^{-rt} \mathrm{d} X(t)\\&=-re^{-rt}X(t) \mathrm{d} t + e^{-rt}\cdot [rX(t) \mathrm{d} t + \\ & \quad \quad \Delta(t)(\alpha-r)S(t) \mathrm{d} t + \Delta(t)\sigma S(t) \mathrm{d} W(t)] \\& = \Delta(t)(\alpha-r)e^{-rt}S(t) \mathrm{d} t + \Delta(t)e^{-rt}\sigma S(t) \mathrm{d} W(t)) \\& = \Delta(t) \mathrm{d} (e^{-rt}S(t))\end{aligned}\end{equation*}$

This equation says that the change in the discounted portfolio value is solely caused by the change in the discounted stock price.

Evolution of option value

Let $c(t,x)$ denote the value of (European) call option at time $t$ when the stock price $x$ , i.e. $c(t,S(t))=(S(t)-K)^+$ , where $K$ is the strike (contract price to buy stock at maturity). Though $c(t,x)$ is a deterministic function, $c(t,S(t))$ has randomness.

By Ito’s formula,

(4) $\begin{equation*}\begin{aligned}\mathrm{d} c(t,S(t)) & = c_t(t,S(t)) \mathrm{d} t + c_x(t,S(t)) \mathrm{d} S(t) + \frac{1}{2}c_{xx}(t,S(t)) \mathrm{d} \langle S,S \rangle_t \\ & = c_t(t,S(t)) \mathrm{d} t + c_x(t,S(t))\ud S(t) + \frac{1}{2}c{xx}(t,S(t)) \sigma^2 S(t)^2 \mathrm{d} t \\& = c_t(t,S(t)) \mathrm{d} t + c_x(t,S(t))(\alpha S(t) \mathrm{d} t + \sigma S(t) \mathrm{d} W(t)) \\ & \quad + \frac{1}{2}c_{xx}(t,S(t)) \sigma^2 S(t)^2 \mathrm{d} t \\& = \left( c_t(t,S) + \alpha c_x(t,S)S + \frac{1}{2}\sigma^2 c_{xx}(t,S) S^2 \right) \mathrm{d} t + \sigma c_x(t,S) S \mathrm{d} W(t)\end{aligned}\end{equation*}$

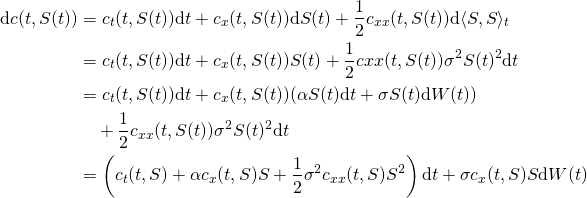
The SDE of the discounted call option value is

(5) $\begin{equation*}\begin{aligned}& \mathrm{d} (e^{-rt}c(t,S(t))) \\ & = -re^{-rt}c(t,S(t)) \mathrm{d} t + e^{-rt} \mathrm{d} c(t,S(t)) \\& = -re^{-rt}c(t,S) \mathrm{d} t + e^{-rt} [ ( c_t(t,S) + \alpha c_x(t,S)S + \\ & \quad \frac{1}{2}\sigma^2 c_{xx}(t,S) S^2 ) \mathrm{d} t + \sigma c_x(t,S) S \mathrm{d} W(t) ] \\& = e^{-rt}[ -rc(t,S) + c_t(t,S) + \alpha c_x(t,S)S + \frac{1}{2}\sigma^2 c_{xx}(t,S) S^2 ] \mathrm{d} t \\ & \quad + e^{-rt}\sigma c_x(t,S) S \mathrm{d} W(t)\end{aligned}\end{equation*}$

Equating portfolio and call option values

To hedge the risk of offering the call option, we hold
a portfolio of equal value at all time $t$ . That is equating the portfolio evolution and the call option evolution.

(6) $\begin{equation*} \begin{aligned}& \mathrm{d}(e^{-rt}X(t)) = \mathrm{d} (e^{-rt}c(t,S(t))) \\& X(0) = c(0,S(0))\end{aligned}\end{equation*}$

It yields

(7) $\begin{equation*} \begin{aligned} & \Delta(t) = c_x(t,S(t)) \\ & rc(t,x) = c_t(t,x) + rc_x(t,x)x + \frac{1}{2}\sigma^2c{xx}(t,x)x^2\end{aligned}\end{equation*}$

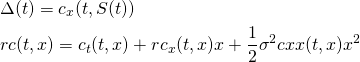
The first equation in (7) is called the delta hedging rule. It says that the number of shares to hold at time $t$ is equal to the partial derivative of option value with respect to the stock price at time $t$ . The second equation in (7) gives the value of the call option.

Suppose we could solve the second PDE in (??) with some proper boundary condition. At $t=0$ we sell the option at price $c(0,S(0))$ . We create a portfolio using this amount of money ( $X(0)$ ) following the delta hedging rule, then the risk of selling the call option is hedged.

We are seeking a continuous solution to the Black-Scholes-Merton partial differential equation

(8) $\begin{equation*} rc(t,x) = c_t(t,x) + rc_x(t,x)x + \frac{1}{2}\sigma^2c_{xx}(t,x)x^2 \ \end{equation*}$

with terminal condition

(9) $\begin{equation*} c(T,x)=(x-K)^+ \end{equation*}$

January 30, 2019August 3, 2019

Volatility

Implied Volatility

Option price in the Black-Scholes-Merton formula can be seen as a function of volatility $\sigma$ if interest rate $r$ and strike price $K$ are known. Market quote of option price gives the volatility which is called implied volatility. Market convention is annualized volatility.

Realized Volatility

Observing the prices of a stock every day in a year, we can compute the realized volatility.

Suppose the stock price follows geometric Brownian Motion, i.e.,

$S(t)=S_0e^{\alpha-\frac{1}{2}\sigma^2t + \sigma W(t)},$

where $W(t)$ is the standard Brownian Motion, and time $t$ takes year as unit.

Then, for $n=1,2, \ldots, 251$ , the number of stock trading days of NYSE in a year.

$\frac{S_{n}}{S_{n-1}} = e^{\frac{\sigma^2}{251}+\sigma\left(W\left(\frac{n}{251}\right)-W\left(\frac{n-1}{251}\right)\right)} \overset{\sD}{=} e^{\frac{\sigma^2}{251}}e^{\sigma W\left(\frac{1}{251}\right)}.$

$\log(\frac{S_{n}}{S_{n-1}}) = \frac{\sigma^2}{251} + \sigma W\left(\frac{1}{251}\right)$

Hence,

$\sigma = \sqrt{251 \cdot \mbox{imperical variance}{\log(\frac{S_{n}}{S_{n-1}})}}.$

Sometimes, people use $\log(x)\sim x-1$ near $x=1$ . In this case,

$\sigma = \sqrt{251 \cdot \mbox{imperical variance}{\frac{S_{n}}{S_{n-1}}}}.$

January 30, 2019January 31, 2019

Geometric Brownian Motion

Denote the stock price at time $t$ by $S(t)$ for $t\geq 0$ . ${S(t),t\geq 0}$ is a stochastic process adapted to a filtration $(\mathcal{F}_t)_{t\geq 0}$ . $W(t)$ is the one-dimensional standard Brownian motion. We assume $S(t)$ satisfies the following stochastic differential equation(SDE):

(1) $\begin{equation*}\mathrm{d} S(t) = \alpha S(t) \mathrm{d} t + \sigma S(t) \mathrm{d} W(t),\end{equation*}$

where $\alpha$ is the return rate of the stock, and $\sigma$ represent the volatility of the stock. The left side of the equation represents the change of stock price, and the right side of the equation is the sum of return and noise that are proportional to the stock price $S(t)$ .

The solution to (1) is a geometric Brownian motion. It can be solved by the following way. Solution to ODE $y'=\alpha y$ is $y(0)e^{\alpha t}$ . It is reasonable to guess the solution to (1) is $S(t)=S(0)e^{at+bW(t)}$ with $a,b$ to be determined. We then apply Ito’s formula to $f(x,y)=e^{ax+by}$ .

$\begin{aligned}\mathrm{d} S(t) = &\ f_x(t,S(t))\mathrm{d} t + f_y(t,S(t))\mathrm{d} W(t) \\& + \frac{1}{2}f_{xx}(t,S(t))\mathrm{d} \langle t,t \rangle + \frac{1}{2} f_{xy}(t,S(t)) \mathrm{d} \langle t,W(t) \rangle + \frac{1}{2}f_{yy}(t,S(t)) \mathrm{d}\langle W,W\rangle_t\\= &\ ae^{at+bW(t)} \mathrm{d} t + be^{at+bW(t)} \mathrm{d} W(t) \\ & + \frac{1}{2}f{xx}(t,S(t)) \mathrm{d} 0+\frac{1}{2}f_{xy}(t,S(t)) \mathrm{d} 0+\frac{1}{2} b^2 e^{at+bW(t)} \mathrm{d} t \\= & \ (a+\frac{1}{2}b^2)e^{at+bW(t)} \mathrm{d} t + be^{at+bW(t)} \mathrm{d} W(t) \\= &\ (a+\frac{1}{2}b^2)S(t) \mathrm{d} t + bS(t) \mathrm{d} W(t)\end{aligned}$

By letting $a+\frac{1}{2}b^2 = \alpha$ and $b= \sigma$ , and solving for $a,b$ , we will get

(2) $\begin{equation*}S(t) = S(0)\exp((\alpha-\frac{1}{2}\sigma^2)t + \sigma W(t)).\end{equation*}$