Month: February 2019

Posted on

Ito’s Formula

Ito’s formula is one of the fundamental tools in stochastic analysis. If the reader is interested in a proof of it, section 5.2 of Le Gull’s Brownian Motion, Martingales, and Stochastic Calculus is a good reference. The idea of the proof is Taylor’s expansion.


Definition: Semi-martingale
Let (\Omega,\mathcal{F},(\mathcal{F}t){t\geq 0},\mathbf{P}) be a filtered probability space. A càdlàg stochastic process (adapted to the filtered probability space) is called a semi-martingale if it can be represented as the sum of a local martingale and a process of locally bounded variation.

Theorem: Ito’s formula for continuous semi-martingales
Let X^1, \ldots, X^n be continuous semi-martingales, and f:\mathbb{R}^n \rightarrow \mathbb{R} , (x_1, \ldots, x_n) \mapsto y, be a \mathcal{C}^2 function. \langle X,Y\rangle denotes the quadratic covariation of continuous semi-martingales X and Y. Then, \forall t>0,

(1)   \begin{equation*} \begin{aligned}\mathrm{d} &f(X^1_t, \ldots, X^n_t) = \sum_{i=1}^{n}\frac{\partial f}{x_i}(X^1_t, \ldots, X^n_t)\mathrm{d} X^i_t \\ & + \frac{1}{2} \sum_{i,j=1}^{n}\frac{\partial^2 f}{x_i x_j}(X^1_t, \ldots, X^n_t) \mathrm{d} \langle X^i,X^j\rangle_t \end{aligned} \end{equation*}

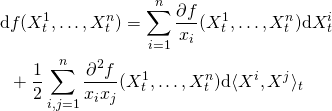
Footnote: càdlàg is an abbreviation of French continue à droite, limite à gauche, which means right continuous with left limits in English. It is a standard abbreviation in stochastic analysis.