March 2019 – Sisi Tang

March 14, 2019March 15, 2019

Gaussian Mixture Model

Gaussian mixture model (GMM) is a probability model for a mixture of several Gaussian distributions with possibly different mean and variance.

For example, we can model the 100m race time of all grade 12 students in a high school as two normal distributions: one for female students and one for male students. It is reasonable to expect two groups have different mean and may different variance.

When to use Gaussian mixture model?

1. Data has more than one clusters.
In the following picture, the left one models the data with one normal distribution; the right one models the data by two normal distribution, Gaussian mixture model. Obviously, the right one better describes the data.

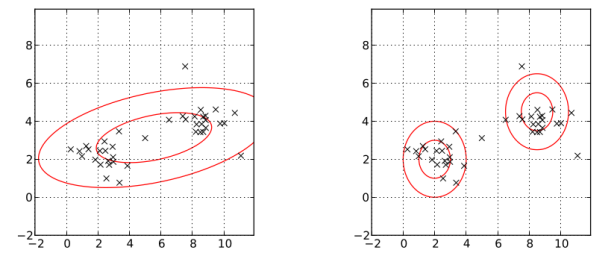
Pictures are from https://brilliant.org/wiki/gaussian-mixture-model/

2. Each cluster is theoretically normally distributed.

Theory of Gaussian Mixture Model

1. Gaussian distribution in 1 dimension
Since there are several Gaussian distributions in the GMM. We assign an index to each Gaussian distribution: $k$ for $k=1,2,..., K$ where K is the number of clusters. For a given mean $\mu_k$ and variance $\sigma_k$ , the probability density function is

$p_k(x|\mu_k,\sigma_k) = \frac{1}{\sigma_k\sqrt{2\pi}}exp\left(-\frac{(x-\mu_k)^2}{2\sigma_k^2}\right)$

Above $|$ is not the mathematical conditional expectation, but a statistical way of saying we know true parameters $\mu_k,\sigma_k$ in advance.

2. Gaussian mixture model in 1 dimension
The probability density function of GMM is the weighted average of several Gaussian densities:

$p(x|\mu_k,\sigma_k, k=1,2,...,K) = \sum_{k=1}^K w_k \cdot p_k(x|\mu_k,\sigma_k ),$

where $w_k \in [0,1]$ satisfies

$\sum_{k=1}^K w_k = 1$

Plug in the Gaussian density,

$p(x) = \sum_{k=1}^K w_k \frac{1}{\sigma_k\sqrt{2\pi}}exp\left(-\frac{(x-\mu_k)^2}{2\sigma_k^2}\right)$

Note that this is a density function because its integral on $\mathbb{R}$ is 1.

3. Gaussian mixture model in n-dimension
Let $x \in \mathbb{R}^n$ be an n-dimension multivariate Gaussian random variable with mean vector
$\mathbf{\mu_k}$ and covariance matrix $\Sigma_k$ . Then the probability density function is

$p_k(x|\mathbf{\mu_k} , \Sigma_k ) = \frac{1}{\sqrt{(2\pi)^K|\Sigma_k|}}exp\left(-\frac{1}{2}(x-\mathbf{\mu}_k)^T\Sigma_k^{-1}(x-\mathbf{\mu}_k )\right)$

Then, the probability density function of GMM, which is the weighted average of serveral multivariate Gaussian density, is

$p(x) = \sum_{k=1}^K w_k \frac{1}{\sqrt{(2\pi)^K|\Sigma_k|}}exp\left(-\frac{1}{2}(x-\mathbf{\mu}_k)^T\Sigma_k^{-1}(x-\mathbf{\mu}_k )\right)$

with

$\sum_{k=1}^K w_k = 1$

Training the Model

Suppose that we know the number of clusters $K$ a priori. (The choice of $K$ relies on statistician’s experience.) Then, we can use Expectation Maximization (EM) algorithm to find the parameters $\hat{w_k}, \hat{\mu_k}$ and $\hat{\sigma_k}$ or $\hat{\Sigma_k}$ for multi-dimensional model. Let $K$ be the number of clusters, and $N$ be the number of samples.

Step 1: Initialize

Randomly choose 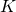$K$ samples and set them to be the group mean. For example, in the case of 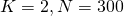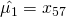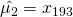$K=2, N=300$ , $\hat{\mu_1} = x_{57}$ , $\hat{\mu_2} = x_{193}$ . (note that this is also valid for multi-dimensional case)
Set all variances (resp. covariance matrices) to be the same value: sample variance (resp. sample covariance matrix). Namely,
$\hat{\sigma_k}^2 = \frac{1}{N}\sum_i^N(x_i-\bar{x})^2,$
where $\bar{x}=\sum_1^Nx_i/N$ .
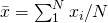Set all weights equal to 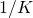$1/K$ , i.e.,
$\hat{w_k} = \frac{1}{K}.$

Step 2: Expectation

We compute the probability that a sample $x_n$ belongs to cluster $C_k$ .

$\begin{aligned} \gamma_{nk} = &~ \mathbf{P}(x_n \in C_k|x_n, \hat{w_k}, \hat{\mu_k},\hat{\sigma_k} ) \\ = &~ \frac{\hat{w_k}p_k(x_n|\hat{\mu_k},\hat{\sigma_k})}{\sum_{j=1}^K \hat{w_j}p_j(x_n|\hat{\mu_j},\hat{\sigma_j}) } \end{aligned}$

Step 3: Maximization

Update parameters then go back to step 2 until converge

$\hat{w_k} = \frac{\sum_{n=1}^N\gamma_{nk}}{N}$
$\hat{\mu_k} = \frac{\sum_{n=1}^N\gamma_{nk}x_i}{ \sum_{n=1}^N\gamma_{nk} }$
$\hat{\sigma_k} = \frac{\sum_{n=1}^N\gamma_{nk}(x_n-\hat{\mu_k} )^2}{ \sum_{n=1}^N\gamma_{nk} }$
resp.
$\hat{\Sigma_k} = \frac{\sum_{n=1}^N\gamma_{nk}(x_n-\hat{\mu_k} )(x_n-\hat{\mu_k} )^T }{ \sum_{n=1}^N\gamma_{nk} }$

March 8, 2019March 8, 2021

European and American Put-Call Parity

We assume no dividend and positive risk-free interest rate.

European put-call parity

European put and call option with same maturity $T$ and strike $K$ satisfy the put-call parity:

$C_E - P_E = S_0 - Ke^{-rT},$

where $C_E$ is the price of European call option, $P_E$ is the price of the European put option, $S_0$ is the price of the underlying asset at time $t=0$ .

$C_E - P_E$ can be seen as a forward contract with maturity $T$ and strike $K$ . A short proof of European put-call parity is as follows:

$(S_T-K)^+ + (K_T-S)^+ = S_T - K$

That is to say the terminal payoff of long call and short put is equal to that of forward (with the same maturity $T$ and strike $K$ ). Hence,

$\begin{aligned}& P(0,T)E[(S_T-K)^+] + P(0,T)E[(K-S_T)^+] \\ & = P(0,T)E[S_T - K],\end{aligned}$

where $P(0,T)$ is the discount factor from $T$ to $0$ , and $E$ is the expectation under the risk neutral measure. Above equation is equivalent to the European put-call parity formula.

Never prematurely exercise American call option

If we wait until maturity, the profit of the call option is $(S_T-K)^+$ . If we exercise the option at time $t$ , then we have $-K$ cash position and a stock the worth $S_t$ at this time. Then, at time $T$ , the total portfolio value would be $S_T-Ke^{r(T-t)}$ . That is

$C_E = C_A$

But if the underlying asset pays a dividend, then it might be optimal to exercise the call option early.

American put-call parity

American put and call option satisfies the following inequality:

$S_0 - K \leq C_A-P_A \leq S_0 - Ke^{-rT}$

For the first inequality,

Suppose at time 0, we have the following portfolio: long a call option, short a put option, short underlying asset, and have $K$ cash.

At $t=0$ , the portfolio value is $C_A - P_A - S_0 + K$ .

If the long position side of the put option decides to exercise the option, we then exercise our call option at the same time, otherwise, wait until maturity to decide exercise or not. With this strategy, call and put has the same exercise time and hence can be seen as a forward with maturity undetermined. Say, the maturity is $t \in [0,T]$ .
Then, at time $t$ , the value of our portfolio is $S_t-K$ for the option part and $-S_t + Ke^{rt}$ for the asset and cash part. The total value of the portfolio is $Ke^{rt} - K > 0$ .

By the non-arbitrage principal, we have

$C_A - P_A - S_0 + K \geq 0$

For the second inequality,

$\begin{aligned} &~ C_A - P_A \\ = &~ C_E - P_E + P_E - P_A \\ = &~ S_0 - K e^{-rT} + P_E - P_A \\ \leq &~ S_0 - Ke^{-rT}\end{aligned}$

March 8, 2019March 8, 2021

European call option v.s. Asian call option

Let a stock follow a Geometric Brownian motion

$\textnormal{d}S_t = S_t(r \textnormal{d} t + \sigma \textnormal{d} W_t)$

with constant $r,\sigma > 0$ . Let

$A_T = \frac{1}{T}\int_0^T S_u \textnormal{d} u$

European Asian call option has the payoff $(A_T-K)^+$ and European vanilla call option has the payoff $(S_T-K)^+$ . Then European vanilla option has higher value.

Proof.

By (1)Jensen’s inequality, (2)Fubini, and (3)the fact that the longer the maturity is the higher the vanilla European option’s value is, we have

$\begin{aligned} &~ \mathbb{E}[e^{-rT}(A_T-K)^+] \\= &~ \mathbb{E}[e^{-rT}(\frac{1}{T}\int_0^T S_u \textnormal{d} u -K)^+] \\\leq & ~ \mathbb{E}[e^{-rT}\frac{1}{T}\int_0^T (S_u-K)^+ \textnormal{d} u] \\= &~ \frac{1}{T}\int_0^T \mathbb{E}[e^{-rT} (S_u-K)^+ ] \textnormal{d} u \\\leq &~ \frac{1}{T}\int_0^T \mathbb{E}[e^{-ru} (S_u-K)^+ ] \textnormal{d} u \\\leq &~ \frac{1}{T}\int_0^T \mathbb{E}[e^{-rT} (S_T-K)^+ ] \textnormal{d} u \\ = &~ \mathbb{E}[e^{-rT} (S_T-K)^+ ] \\ \end{aligned}$

Notice that we didn’t use the dynamics of Geometric Brownian motion. Above deduction is true as long as (3) is true.