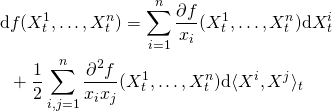Feynman-Kac formula connects the solution to a SDE to the solution of a PDE. For example, the Black-Scholes formula is an application of Feynman-Kac.
Let ![]() satisfies the following SDE driven by standard Brownian Motion:
satisfies the following SDE driven by standard Brownian Motion:
![]()
Let ![]() be a Borel measurable function, and
be a Borel measurable function, and ![]() . Define
. Define
![Rendered by QuickLaTeX.com \[\begin{aligned} g(t,x) := \mathbf{E} [&\int_t^Te^{-\int_t^TV(\tau,X_{\tau})\textnormal{d}\tau}f(r,X_r)\textnormal{d}r \\ &+e^{-\int_t^TV(\tau,X_{\tau})}h(X_T)|X_t = x ] \end{aligned}.\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-ce949eee9441cd7cb71600b656d22116_l3.png)
Then, ![]() satisfies PDE
satisfies PDE
![]()
Proof.
To get an idea of how this formula is proved, we start with a base case. The general case is proved by the same manner with a little more complicated calculation.
Suppose ![]() .
.
Let ![]() be the natural filtration associated with the standard Brownian Motion in the SDE. By the Markov property of the solution to SDE, we have
be the natural filtration associated with the standard Brownian Motion in the SDE. By the Markov property of the solution to SDE, we have ![]() ,
,
![]()
Then, for ![]()
![]()
Hence, ![]() is a martingale.
is a martingale.
Then, we apply Ito’s formula to ![]() . Its drift term should be zero because it is a martingale. This leads to the Feynman-Kac PDE.
. Its drift term should be zero because it is a martingale. This leads to the Feynman-Kac PDE.
![Rendered by QuickLaTeX.com \[\begin{aligned} \textnormal{d}g(t,X_t) & = g_t\textnormal{d}t + g_x \textnormal{d} x + \frac{1}{2}g_{xx} \textnormal{d} X \textnormal{d} X \\ & = [g_t+\beta g_x + \frac{1}{2}\gamma^2 g_{xx}] \textnormal{d} t + \gamma g_x \textnormal{d} W\end{aligned}.\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-91595ea304137e12671716f319367ebf_l3.png)
By setting the ![]() term equal to
term equal to ![]() , we get the PDE:
, we get the PDE:
![]()
For the general case, we only need to factor out the ![]() integral and make the integral inside the expectation only contains
integral and make the integral inside the expectation only contains ![]() term. We will get
term. We will get ![]() is a martingale with
is a martingale with ![]() defined as:
defined as:
![]()
Similarly, by applying Ito’s formula to above martingale and setting the drift term equal to 0, we will get the result.

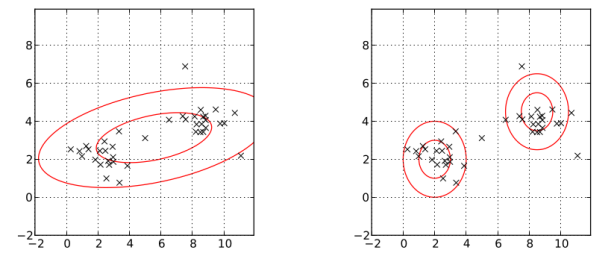
![Rendered by QuickLaTeX.com \[p(x|\mu_k,\sigma_k, k=1,2,...,K) = \sum_{k=1}^K w_k \cdot p_k(x|\mu_k,\sigma_k ),\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-43a9821781ab30977d08dc18bed86dcd_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^K w_k = 1\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-1cbe2e8d5a2ce1f1fcaef3e32fe7c455_l3.png)
![Rendered by QuickLaTeX.com \[p(x) = \sum_{k=1}^K w_k \frac{1}{\sigma_k\sqrt{2\pi}}exp\left(-\frac{(x-\mu_k)^2}{2\sigma_k^2}\right)\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-a657f7bc6c42e9486be0ba6c7a0cf787_l3.png)
![Rendered by QuickLaTeX.com \[p(x) = \sum_{k=1}^K w_k \frac{1}{\sqrt{(2\pi)^K|\Sigma_k|}}exp\left(-\frac{1}{2}(x-\mathbf{\mu}_k)^T\Sigma_k^{-1}(x-\mathbf{\mu}_k )\right)\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-cc5be764062ddb791b6882bc4e93a1f4_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\sigma_k}^2 = \frac{1}{N}\sum_i^N(x_i-\bar{x})^2,\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-19025e84c2b88d0c995e301952199ca8_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned} \gamma_{nk} = &~ \mathbf{P}(x_n \in C_k|x_n, \hat{w_k}, \hat{\mu_k},\hat{\sigma_k} ) \\ = &~ \frac{\hat{w_k}p_k(x_n|\hat{\mu_k},\hat{\sigma_k})}{\sum_{j=1}^K \hat{w_j}p_j(x_n|\hat{\mu_j},\hat{\sigma_j}) } \end{aligned} \]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-9061aaabea11b55f164405f44bb9f7fa_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\mu_k} = \frac{\sum_{n=1}^N\gamma_{nk}x_i}{ \sum_{n=1}^N\gamma_{nk} }\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-e919444d875e3723786da4b77f4bbd6c_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\sigma_k} = \frac{\sum_{n=1}^N\gamma_{nk}(x_n-\hat{\mu_k} )^2}{ \sum_{n=1}^N\gamma_{nk} }\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-d67e2738e34303acd3a6c5572cecf3fd_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\Sigma_k} = \frac{\sum_{n=1}^N\gamma_{nk}(x_n-\hat{\mu_k} )(x_n-\hat{\mu_k} )^T }{ \sum_{n=1}^N\gamma_{nk} }\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-5e899bee111b8a4c25f9e0629a6aacec_l3.png)