We assume no dividend and positive risk-free interest rate.
European put-call parity
European put and call option with same maturity 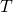 and strike
and strike 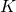 satisfy the put-call parity:
satisfy the put-call parity:
![Rendered by QuickLaTeX.com \[C_E - P_E = S_0 - Ke^{-rT},\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-003d36a4381615a4a8a6bcd91633509a_l3.png)
where 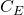 is the price of European call option,
is the price of European call option, 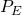 is the price of the European put option,
is the price of the European put option, 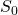 is the price of the underlying asset at time
is the price of the underlying asset at time 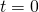 .
.
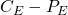 can be seen as a forward contract with maturity
can be seen as a forward contract with maturity 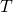 and strike
and strike 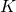 . A short proof of European put-call parity is as follows:
. A short proof of European put-call parity is as follows:
![Rendered by QuickLaTeX.com \[(S_T-K)^+ + (K_T-S)^+ = S_T - K\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-600c329621a498f24fd142f948b7bb87_l3.png)
That is to say the terminal payoff of long call and short put is equal to that of forward (with the same maturity 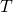 and strike
and strike 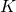 ). Hence,
). Hence,
![Rendered by QuickLaTeX.com \[\begin{aligned}& P(0,T)E[(S_T-K)^+] + P(0,T)E[(K-S_T)^+] \\ & = P(0,T)E[S_T - K],\end{aligned}\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-5eb6438c9f251d8cb7314f091d271dbf_l3.png)
where 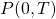 is the discount factor from
is the discount factor from 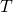 to
to 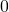 , and
, and 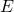 is the expectation under the risk neutral measure. Above equation is equivalent to the European put-call parity formula.
is the expectation under the risk neutral measure. Above equation is equivalent to the European put-call parity formula.
Never prematurely exercise American call option
If we wait until maturity, the profit of the call option is 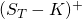 . If we exercise the option at time
. If we exercise the option at time 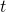 , then we have
, then we have 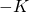 cash position and a stock the worth
cash position and a stock the worth 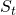 at this time. Then, at time
at this time. Then, at time 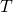 , the total portfolio value would be
, the total portfolio value would be 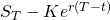 . That is
. That is
![Rendered by QuickLaTeX.com \[C_E = C_A\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-ef54a410567895cf99f23891f2fa60cd_l3.png)
But if the underlying asset pays a dividend, then it might be optimal to exercise the call option early.
American put-call parity
American put and call option satisfies the following inequality:
![Rendered by QuickLaTeX.com \[S_0 - K \leq C_A-P_A \leq S_0 - Ke^{-rT}\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-9622a321de5ca93455cf7c501e98e96e_l3.png)
For the first inequality,
Suppose at time 0, we have the following portfolio: long a call option, short a put option, short underlying asset, and have 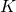 cash.
cash.
At 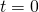 , the portfolio value is
, the portfolio value is 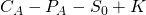 .
.
If the long position side of the put option decides to exercise the option, we then exercise our call option at the same time, otherwise, wait until maturity to decide exercise or not. With this strategy, call and put has the same exercise time and hence can be seen as a forward with maturity undetermined. Say, the maturity is ![Rendered by QuickLaTeX.com t \in [0,T]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-e88dbf1b3766ac724ea7ac1993e27abb_l3.png) .
.
Then, at time 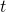 , the value of our portfolio is
, the value of our portfolio is 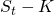 for the option part and
for the option part and 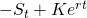 for the asset and cash part. The total value of the portfolio is
for the asset and cash part. The total value of the portfolio is 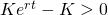 .
.
By the non-arbitrage principal, we have
![Rendered by QuickLaTeX.com \[C_A - P_A - S_0 + K \geq 0\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-777e90a48cc26e26872082fe5661d0c5_l3.png)
For the second inequality,
![Rendered by QuickLaTeX.com \[\begin{aligned} &~ C_A - P_A \\ = &~ C_E - P_E + P_E - P_A \\ = &~ S_0 - K e^{-rT} + P_E - P_A \\ \leq &~ S_0 - Ke^{-rT}\end{aligned}\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-fe1a798b995e50876a2ad42b955381b4_l3.png)

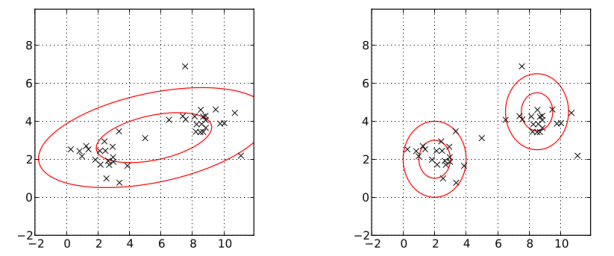
![Rendered by QuickLaTeX.com \[p(x|\mu_k,\sigma_k, k=1,2,...,K) = \sum_{k=1}^K w_k \cdot p_k(x|\mu_k,\sigma_k ),\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-43a9821781ab30977d08dc18bed86dcd_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^K w_k = 1\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-1cbe2e8d5a2ce1f1fcaef3e32fe7c455_l3.png)
![Rendered by QuickLaTeX.com \[p(x) = \sum_{k=1}^K w_k \frac{1}{\sigma_k\sqrt{2\pi}}exp\left(-\frac{(x-\mu_k)^2}{2\sigma_k^2}\right)\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-a657f7bc6c42e9486be0ba6c7a0cf787_l3.png)
![Rendered by QuickLaTeX.com \[p(x) = \sum_{k=1}^K w_k \frac{1}{\sqrt{(2\pi)^K|\Sigma_k|}}exp\left(-\frac{1}{2}(x-\mathbf{\mu}_k)^T\Sigma_k^{-1}(x-\mathbf{\mu}_k )\right)\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-cc5be764062ddb791b6882bc4e93a1f4_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\sigma_k}^2 = \frac{1}{N}\sum_i^N(x_i-\bar{x})^2,\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-19025e84c2b88d0c995e301952199ca8_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned} \gamma_{nk} = &~ \mathbf{P}(x_n \in C_k|x_n, \hat{w_k}, \hat{\mu_k},\hat{\sigma_k} ) \\ = &~ \frac{\hat{w_k}p_k(x_n|\hat{\mu_k},\hat{\sigma_k})}{\sum_{j=1}^K \hat{w_j}p_j(x_n|\hat{\mu_j},\hat{\sigma_j}) } \end{aligned} \]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-9061aaabea11b55f164405f44bb9f7fa_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\mu_k} = \frac{\sum_{n=1}^N\gamma_{nk}x_i}{ \sum_{n=1}^N\gamma_{nk} }\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-e919444d875e3723786da4b77f4bbd6c_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\sigma_k} = \frac{\sum_{n=1}^N\gamma_{nk}(x_n-\hat{\mu_k} )^2}{ \sum_{n=1}^N\gamma_{nk} }\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-d67e2738e34303acd3a6c5572cecf3fd_l3.png)
![Rendered by QuickLaTeX.com \[\hat{\Sigma_k} = \frac{\sum_{n=1}^N\gamma_{nk}(x_n-\hat{\mu_k} )(x_n-\hat{\mu_k} )^T }{ \sum_{n=1}^N\gamma_{nk} }\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-5e899bee111b8a4c25f9e0629a6aacec_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned} &~ C_A - P_A \\ = &~ C_E - P_E + P_E - P_A \\ = &~ S_0 - K e^{-rT} + P_E - P_A \\ \leq &~ S_0 - Ke^{-rT}\end{aligned}\]](https://sisitang0.com/wp-content/ql-cache/quicklatex.com-fe1a798b995e50876a2ad42b955381b4_l3.png)