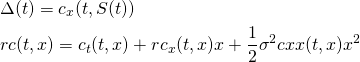Sisi Tang – Page 5 – A Quantitative Finance Website

February 3, 2019March 8, 2021

Bond Yield v.s. Bond Price

When our study group read John Hull’s Options, Futures, and Other Derivatives book section 4.10 Duration, there was a sentence that is not very intuitive: There is a negative relationship between bond yield and bond price. (When bond yields decrease, bond prices increase. When bond yields increase, bond price decrease.)

Intuitively, people would believe a high “yield” bond has high price. Here is an explanation to the anti-intuition fact.

Assumption
Suppose the coupon rate and time of payments of a bond are fixed. (It is fixed the time it is designed.) Namely, at time $t_1, \ldots, t_n$ , the bond holder will receive $c_1, \ldots, c_n$ dollars. The last payment $c_n$ contains the
notional/face value of the bond. At time $t=0$ , maket has a quote $B$ of this bond, i.e., how much people are willing to pay for this bond.

Formulation
Bond yield $y$ is defined as the discount rate such that the sum of the present values of all payments is equal to the bond price $B$ . That is to say, $y$ is solved from the following equation:

$B = \sum_{i=1}^n c_ie^{-yt_i}$

In the above equation, there are only two variables $y$ and $B$ . Hence, $B$ is a function of $y$ and vice versa.

$B=B(y)$

Then,

$\mathrm{d}B = \frac{ \mathrm{d} B}{ \mathrm{d} y} \mathrm{d}y.$

No partial derivatives because $c_i$ and $t_i$ are fixed. They are not variables.

Approximately, small change $\Delta y$ in bond yield would result in the change of the bond price being approximately

$\Delta B = \frac{ \mathrm{d} B}{ \mathrm{d} y} \Delta y.$

That is,

$\Delta B = -\sum_{i=1}^n c_it_ie^{-yt_i} \Delta y.$

Duration of a bond is defined to be the weighted average of the time of coupon payments and notional, where the weight is the present value. Namely,

$D := \sum_{i=1}^n t_i\left[\frac{c_ie^{-yt_i}}{B}\right]$

Plug this into the equation of $\Delta B$ , we get

$\Delta B = - BD \Delta y.$

Explanation
Mathematically, if $\Delta y$ is positive, then $\Delta B$ is negative. If $\Delta y$ is negative, then $\Delta B$ is positive.
Intuitively, bond yield and bond price are two ways to quote a bond; just like in describing fuel efficiency, you can use miles/gallon or liters/hundred miles. There is a one to one correspondence between bond yield and bond price. Higher bond yield is corresponding to a lower bond price. We can not say higher bond yield results in lower bond price.

The usual “yield” in people’s mind is actually coupon rate. Higher coupon rate definitely results in higher bond price (if other conditions keep the same).

The market usually quotes bond yield. People can get the approximated bond price change by the formula $\Delta B = - BD \Delta y$ .

What causes the change of a bond price?
Change of interest rate (risk-free rate).
If the interest rate rockets, then the present value of a payment in the future will worth less money. Then, th bond price, which is the sum of present values of all payments in the future, will decrease.

February 1, 2019February 1, 2019

Ito’s Formula

Ito’s formula is one of the fundamental tools in stochastic analysis. If the reader is interested in a proof of it, section 5.2 of Le Gull’s Brownian Motion, Martingales, and Stochastic Calculus is a good reference. The idea of the proof is Taylor’s expansion.

Definition: Semi-martingale
Let $(\Omega,\mathcal{F},(\mathcal{F}t){t\geq 0},\mathbf{P})$ be a filtered probability space. A càdlàg stochastic process (adapted to the filtered probability space) is called a semi-martingale if it can be represented as the sum of a local martingale and a process of locally bounded variation.

Theorem: Ito’s formula for continuous semi-martingales
Let $X^1, \ldots, X^n$ be continuous semi-martingales, and $f:\mathbb{R}^n \rightarrow \mathbb{R} , (x_1, \ldots, x_n) \mapsto y$ , be a $\mathcal{C}^2$ function. $\langle X,Y\rangle$ denotes the quadratic covariation of continuous semi-martingales $X$ and $Y$ . Then, $\forall t>0$ ,

(1) $\begin{equation*} \begin{aligned}\mathrm{d} &f(X^1_t, \ldots, X^n_t) = \sum_{i=1}^{n}\frac{\partial f}{x_i}(X^1_t, \ldots, X^n_t)\mathrm{d} X^i_t \\ & + \frac{1}{2} \sum_{i,j=1}^{n}\frac{\partial^2 f}{x_i x_j}(X^1_t, \ldots, X^n_t) \mathrm{d} \langle X^i,X^j\rangle_t \end{aligned} \end{equation*}$

Footnote: càdlàg is an abbreviation of French continue à droite, limite à gauche, which means right continuous with left limits in English. It is a standard abbreviation in stochastic analysis.

January 31, 2019August 3, 2019

Derivation of Black-Scholes-Merton Formula

The derivation of the Black-Scholes-Merton formula is very clearly organized in section 4.5 of Shreve’s Stochastic Calculus for Finance II Continuous-Time Models. It is the most intuitive and clearest way that the author has seen so far. So, this part especially the organization of the article is borrowed from it though not identical.

Evolution of portfolio value

Let $X(t)$ represent the portfolio value at time $t$ .

We hold $\Delta(t)$ shares of the stock at time $t$ , and put the rest of money in money market with interest rate $r$ . Note that $\Delta(t)$ is adapted to the natural filtration of $W(t)$ . Then, the change of portfolio value is the change in stock plus the interest from money market. To be specific $X(t)$ satisfies the following SDE:

(1) $\begin{equation*} \ud X(t) = \Delta(t)\ud S(t) + r(X(t)-\Delta(t)S(t))\ud t \end{equation*}$

We plug Geometric Brownian motion $S(t)$ into this equation,

$\begin{aligned}\ud X(t) &= \Delta(t)(\alpha S(t) \ud t + \sigma S(t) \ud W(t)) + r(X(t)-\Delta(t)S(t))\ud t \\&= rX(t)\ud t + \Delta(t)(\alpha-r)S(t)\ud t + \Delta(t)\sigma S(t)\ud W(t).\end{aligned}$

The SDE of the discounted stock value $e^{-rt}S(t)$ is obtained by Ito’s formula.

(2) $\begin{equation*}\begin{aligned}\mathrm{d}(e^{-rt}S(t)) &= -re^{-rt}S(t) \mathrm{d} t + e^{-rt} \mathrm{d} S(t) + 0 + 0 + 0 \\&= -re^{-rt}S(t) \mathrm{d} t + e^{-rt} (\alpha S(t) \mathrm{d} t + \sigma S(t) \mathrm{d} W(t)) \\&= (\alpha-r)e^{-rt}S(t) \mathrm{d} t + \sigma e^{-rt} S(t) \mathrm{d} W(t)\end{aligned}\end{equation*}$

This equation says that discounting the stock price reduces the mean return rate from $\alpha$ to $\alpha-r$ .

Similarly, the SDE of the discounted portfolio value $e^{-rt}X(t)$ is

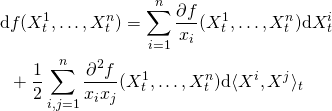
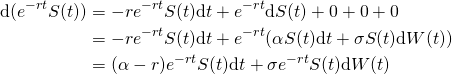
(3) $\begin{equation*}\begin{aligned}\mathrm{d} (e^{-rt}X(t))& = -re^{-rt}X(t) \mathrm{d} t + e^{-rt} \mathrm{d} X(t)\\&=-re^{-rt}X(t) \mathrm{d} t + e^{-rt}\cdot [rX(t) \mathrm{d} t + \\ & \quad \quad \Delta(t)(\alpha-r)S(t) \mathrm{d} t + \Delta(t)\sigma S(t) \mathrm{d} W(t)] \\& = \Delta(t)(\alpha-r)e^{-rt}S(t) \mathrm{d} t + \Delta(t)e^{-rt}\sigma S(t) \mathrm{d} W(t)) \\& = \Delta(t) \mathrm{d} (e^{-rt}S(t))\end{aligned}\end{equation*}$

This equation says that the change in the discounted portfolio value is solely caused by the change in the discounted stock price.

Evolution of option value

Let $c(t,x)$ denote the value of (European) call option at time $t$ when the stock price $x$ , i.e. $c(t,S(t))=(S(t)-K)^+$ , where $K$ is the strike (contract price to buy stock at maturity). Though $c(t,x)$ is a deterministic function, $c(t,S(t))$ has randomness.

By Ito’s formula,

(4) $\begin{equation*}\begin{aligned}\mathrm{d} c(t,S(t)) & = c_t(t,S(t)) \mathrm{d} t + c_x(t,S(t)) \mathrm{d} S(t) + \frac{1}{2}c_{xx}(t,S(t)) \mathrm{d} \langle S,S \rangle_t \\ & = c_t(t,S(t)) \mathrm{d} t + c_x(t,S(t))\ud S(t) + \frac{1}{2}c{xx}(t,S(t)) \sigma^2 S(t)^2 \mathrm{d} t \\& = c_t(t,S(t)) \mathrm{d} t + c_x(t,S(t))(\alpha S(t) \mathrm{d} t + \sigma S(t) \mathrm{d} W(t)) \\ & \quad + \frac{1}{2}c_{xx}(t,S(t)) \sigma^2 S(t)^2 \mathrm{d} t \\& = \left( c_t(t,S) + \alpha c_x(t,S)S + \frac{1}{2}\sigma^2 c_{xx}(t,S) S^2 \right) \mathrm{d} t + \sigma c_x(t,S) S \mathrm{d} W(t)\end{aligned}\end{equation*}$

The SDE of the discounted call option value is

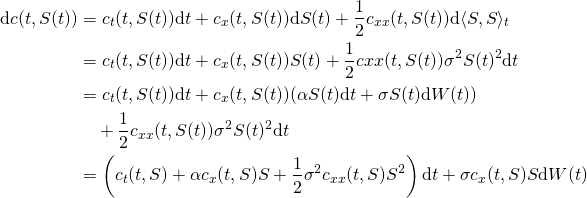
(5) $\begin{equation*}\begin{aligned}& \mathrm{d} (e^{-rt}c(t,S(t))) \\ & = -re^{-rt}c(t,S(t)) \mathrm{d} t + e^{-rt} \mathrm{d} c(t,S(t)) \\& = -re^{-rt}c(t,S) \mathrm{d} t + e^{-rt} [ ( c_t(t,S) + \alpha c_x(t,S)S + \\ & \quad \frac{1}{2}\sigma^2 c_{xx}(t,S) S^2 ) \mathrm{d} t + \sigma c_x(t,S) S \mathrm{d} W(t) ] \\& = e^{-rt}[ -rc(t,S) + c_t(t,S) + \alpha c_x(t,S)S + \frac{1}{2}\sigma^2 c_{xx}(t,S) S^2 ] \mathrm{d} t \\ & \quad + e^{-rt}\sigma c_x(t,S) S \mathrm{d} W(t)\end{aligned}\end{equation*}$

Equating portfolio and call option values

To hedge the risk of offering the call option, we hold
a portfolio of equal value at all time $t$ . That is equating the portfolio evolution and the call option evolution.

(6) $\begin{equation*} \begin{aligned}& \mathrm{d}(e^{-rt}X(t)) = \mathrm{d} (e^{-rt}c(t,S(t))) \\& X(0) = c(0,S(0))\end{aligned}\end{equation*}$

It yields

(7) $\begin{equation*} \begin{aligned} & \Delta(t) = c_x(t,S(t)) \\ & rc(t,x) = c_t(t,x) + rc_x(t,x)x + \frac{1}{2}\sigma^2c{xx}(t,x)x^2\end{aligned}\end{equation*}$

The first equation in (7) is called the delta hedging rule. It says that the number of shares to hold at time $t$ is equal to the partial derivative of option value with respect to the stock price at time $t$ . The second equation in (7) gives the value of the call option.

Suppose we could solve the second PDE in (??) with some proper boundary condition. At $t=0$ we sell the option at price $c(0,S(0))$ . We create a portfolio using this amount of money ( $X(0)$ ) following the delta hedging rule, then the risk of selling the call option is hedged.

We are seeking a continuous solution to the Black-Scholes-Merton partial differential equation

(8) $\begin{equation*} rc(t,x) = c_t(t,x) + rc_x(t,x)x + \frac{1}{2}\sigma^2c_{xx}(t,x)x^2 \ \end{equation*}$

with terminal condition

(9) $\begin{equation*} c(T,x)=(x-K)^+ \end{equation*}$